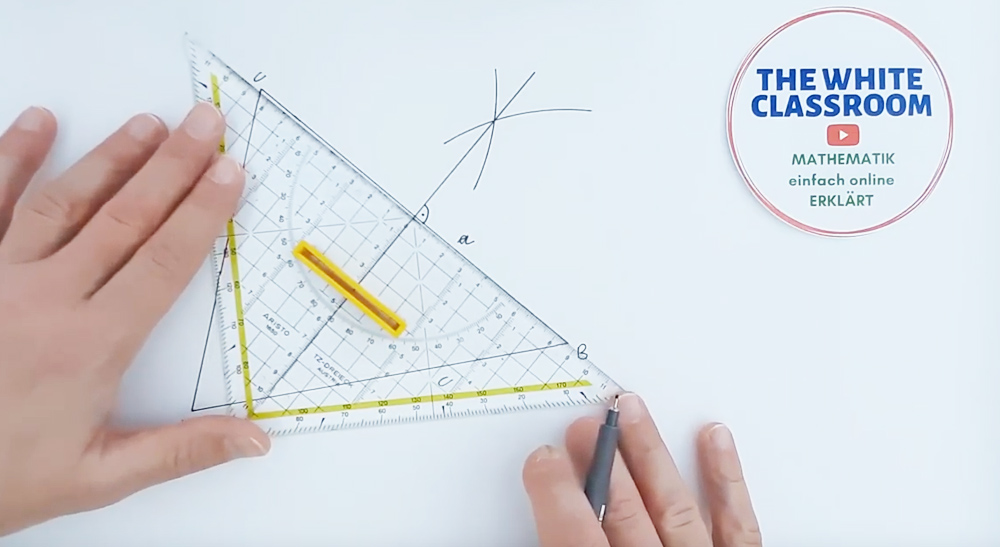
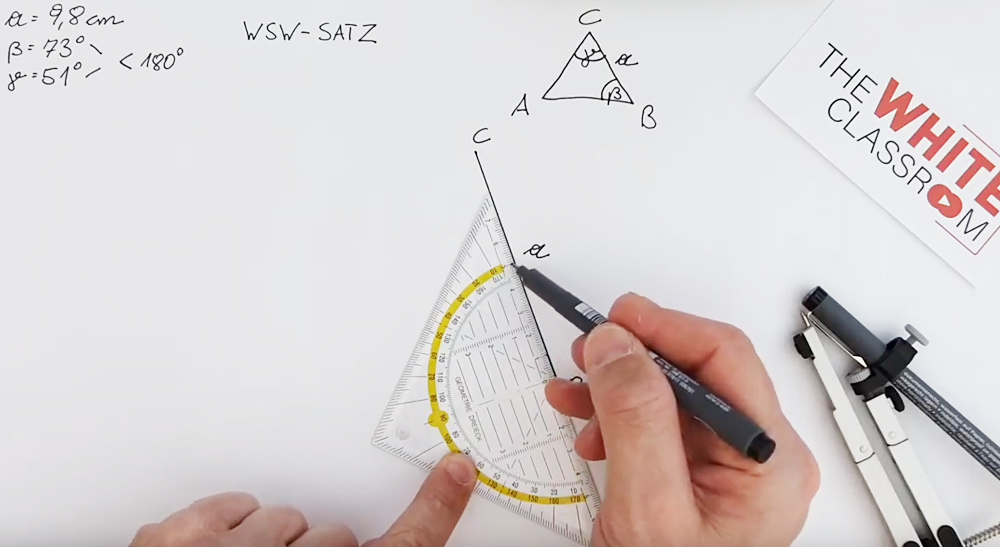
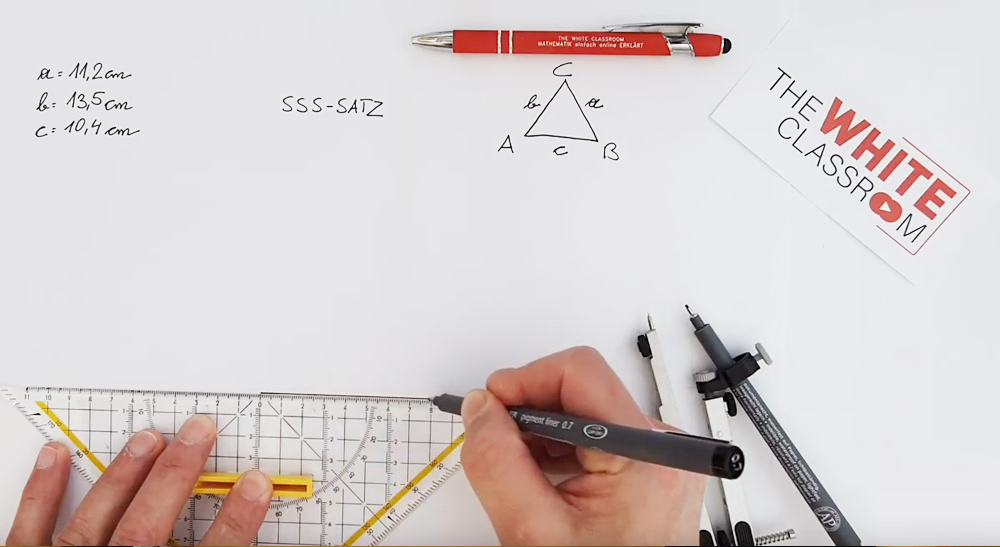
4.8Anwendungsbeispiel 1 - Konstruktion aller 4 Punkte + e - Gerade
Die Euler´sche Gerade ist nach Leonhard Euler benannt.
Auf der Euler´schen Geraden liegen U,S und H.
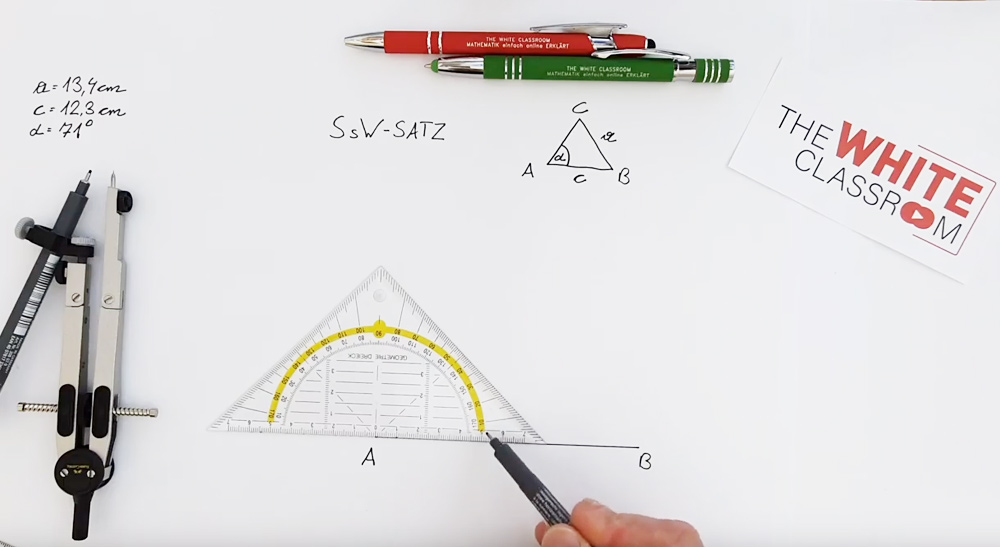
D1 - Konstruktion des Dreiecks aus Seite a, Seite b und Winkel γ (SWS Satz)
Konstruiere folgendes spitzwinkelige Dreieck:
a = 113 mm, b = 155 mm, γ (gamma) = 56°
und miss die fehlende Seite "c" ab.
D1 - Konstruktion des Höhenschnittpunkts: Miss die Längen der 3 Höhen ab!
Fortsetzungsbeispiel:
Konstruiere in folgendes spitzwinkelige Dreieck den Höhenschnittpunkt:
a = 113 mm, b = 155 mm, γ (gamma) = 56°
und miss die 3 Höhen (ha, hb, hc) ab.
D1 - Konstruktion von U, S und I im spitzwinkeligen Dreiecköhenschnittpunkts: Miss die Längen der 3 Höhen ab!
Fortsetzungsbeispiel:
Konstruiere in folgendes spitzwinkelige Dreieck
den Umkreismittelpunkt, den Schwerpunkt und den Inkreismittelpunkt:a = 113 mm, b = 155 mm, γ (gamma) = 56°
D1 - Konstruktion des Umkreises und des Inkreises sowie der Eulerschen Gerade
Fortsetzungsbeispiel:
Konstruiere in folgendes spitzwinkelige Dreieck den
Umkreis und den Inkreis, sowie die Eulersche Gerade!a = 113 mm, b = 155 mm, γ (gamma) = 56°