4.4Konstruktion nach dem SWS - Satz (Seite, Winkel, Seite)
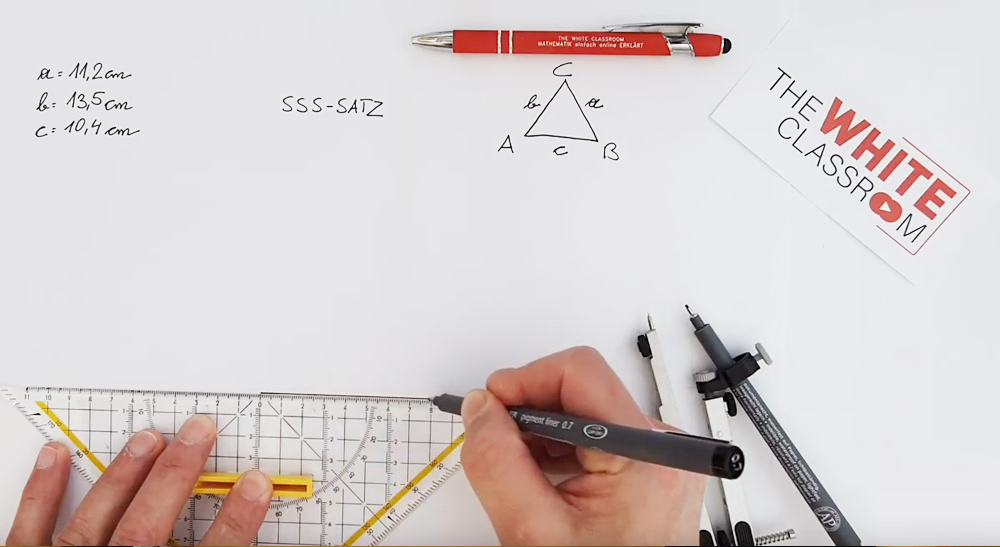
SWS-Satz (Seiten-Winkel-Seitensatz): Dreiecke sind kongruent, wenn sie in zwei Seiten und dem eingeschlossenen Winkel übereinstimmen.
Kongruenzsatz (SWS - Satz / Seite, Winkel, Seite) - b = 9,4 cm, c = 11 cm, α (alpha) = 53°
Konstruiere mit Hilfe des SWS - Satzes folgendes Dreieck:
b = 9,4 cm, c = 11 cm, α (alpha) = 53°
Kongruenzsatz (SWS - Satz / Seite, Winkel, Seite) - b = 5,7 cm, c = 8,4 cm, α (alpha) = 123°
Konstruiere mit Hilfe des SWS - Satzes folgendes Dreieck:
b = 5,7 cm, c = 8,4 cm, α (alpha) = 123°
Kongruenzsatz (SWS - Satz / Seite, Winkel, Seite) - a = 10,5 cm, c = 12 cm, β (beta) = 67°
Konstruiere mit Hilfe des SWS - Satzes folgendes Dreieck:
a = 10,5 cm, c = 12 cm, β (beta) = 67°
Kongruenzsatz (SWS - Satz / Seite, Winkel, Seite) - a = 8,5 cm, c = 9,7 cm, β (beta) = 121°
Konstruiere mit Hilfe des SWS - Satzes folgendes Dreieck:
a = 8,5 cm, c = 9,7 cm, β (beta) = 121°
Kongruenzsatz (SWS - Satz / Seite, Winkel, Seite) - a = 10 cm, b = 12,3 cm, γ (gamma) = 47°
Konstruiere mit Hilfe des SWS - Satzes folgendes Dreieck:
a = 10 cm, b = 12,3 cm, γ (gamma) = 47°
Kongruenzsatz (SWS - Satz / Seite, Winkel, Seite) - a = 6,3 cm, b = 7,4 cm, γ (gamma) = 133°
Konstruiere mit Hilfe des SWS - Satzes folgendes Dreieck:
a = 6,3 cm, b = 7,4 cm, γ (gamma) = 133°